Because of the roughness (inevitably present in most natural and engineering
surfaces), when being brought in contact, solids touch over multitude of separate
”islands” forming the true contact area, which in general is considerably smaller than the
nominal contact area. The true contact area strongly affects almost all facets of interfacial
physics such as stress state, friction, adhesion, wear, and also transport of energy across
and transport of mass along the interface. Using advanced numerical simulations, we
study how the contact area grows under increasing pressure for different material and
roughness parameters [1,2]. In this context, we will discuss some details of generation
of synthetic fractal surfaces, their characterization and the interplay of parameters : root
mean squared height and slope, Nayak’s parameter, Gaussianity, cutoff wavelengths and
fractal dimension. Notably, we will demonstrate the effect of higher spectral moments
of the roughness on the evolution of the contact area, which were missed in previous
studies.
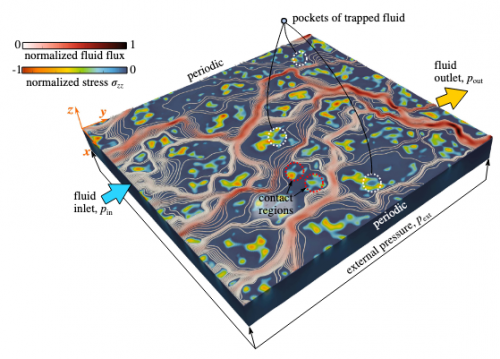In the second part, we will discuss the viscous fluid flow in contact interfaces within a
one-way (weak) coupling formulation and also within a recently constructed monolithic
finite element framework for strong coupling between fluid and solid mechanics in contact
interfaces [3].
Notably, the effect of fluid entrapment in contact pockets will be discussed
[4]. Self-consistent homogenization techniques and drawbacks of the simple geometrical
overlap models for gap-field estimation will be discussed. Finally, first results on the
thermomechanical coupling in rough contact interfaces will be presented.
Figure 1 : Creeping fluid flow in contact interface between rough surfaces simulated using strongly coupled monolithic finite element framework.
References
[1] V.A. Yastrebov, G. Anciaux, J.F. Molinari, From infinitesimal to full contact between
rough surfaces : evolution of the contact area, Int. J. Solids Struct., 52:83-102 (2015)
[2] V.A. Yastrebov, G. Anciaux, J.F Molinari, The role of the roughness spectral breadth in
elastic contact of rough surfaces, J. Mech. Phys. Solids, 107:469-493 (2017)
[3] A.G. Shvarts, J. Vignollet, V.A. Yastrebov. ”Computational framework for monolithic
coupling for thin fluid flow in contact interfaces”. Comp. Meth. App. Mech. Eng.,
379:113738 (2021)
[4] A.G. Shvarts, V.A. Yastrebov. ”Trapped fluid in contact interface”. J. Mech. Phys.
Solids, 119:140-162 (2018).
