L’approche développée ici, concerne principalement les problèmes inverses non linéaires en acoustique et plus précisément, la détermination des caractéristiques géométriques et physiques de milieux complexes (géométrie et/ou composition).

Une des particularités de l’approche mise en oeuvre est qu’elle ne permet pas d’expliciter la solution sous la forme d’une fonction linéaire des données du problème, contrairement à ce qui se fait de façon plus traditionnelle dans les algorithmes de Tomographie basés sur des approximations de Born, Born Distordu, Born itératif, ... . La méthodologie consiste à définir une fonction coût (notée par la suite) dépendant de l’écart - dans une norme choisie - entre le champ acoustique "mesuré" (considéré comme une donnée du problème) et le champ acoustique "calculé" via un modèle numérique d’interaction onde - obstacle (plus, en général, un terme de pénalité destiné à stabiliser le problème). La recherche des minima de cette fonctionnelle (en général – pour ce type de problème – la solution n’est pas unique) nécessite alors la résolution d’un problème direct pour chaque "jeu" de paramètres testés (Fig.1).

Fig.1 : algorithme d’inversion.

Nous nous focalisons principalement sur cinq difficultés :

1) la recherche d’une expression de fonction coût adaptée, choix déterminant dans la procédure de recherche des zéros ou des minima (recherche locale ou globale d’une solution) ;

2) la "discrimination" des solutions générées parmi l’ensemble des minima que possède la fonction coût. Le choix d’une solution particulière peut se faire par post-traitement ou en choisissant une forme particulière de la fonction coût. C’est sur ces deux options que portent nos efforts récents ;

3) l’étude de la sensibilité des reconstructions paramétriques vis-à-vis des erreurs numériques des données (problème mal posé) ;

4) le choix d’un modèle "estimateur’’ pour la résolution du problème direct pendant l’inversion et les conséquences portant notamment sur les notions "d’inadéquation de modèle" et de "crime inverse" ;

5) la reconstruction simultanée de plusieurs paramètres indépendants caractérisant complètement la géométrie et la composition des milieux sondés.

I. Position du problème.

La configuration est celle présentée dans la Fig.(2) ci dessous. L’espace est divisé en deux régions : (non borné) et de frontière régulière. L’origine du référentiel se trouve à l’intérieur de . représentent les potentiels de vitesses ou pressions incidents, diffractés, totaux. Ces potentiels ou pressions ne dépendent pas de z.

Fig.2 : configuration générale

Le problème mathématique est le suivant :

Enfin, on utilise une représentation du champ en ondes partielles :

Le problème direct consiste à déterminer , en tout point de l’espace connaissant , , , , , , et  ; le problème inverse consiste à déterminer un ou plusieurs paramètres du milieu , i.e., , , , , connaissant , en un ensemble de points régulièrement répartis sur une portion ou la totalité d’une surface () entourant complètement l’objet sondé.

II. Problème inverse de frontière.

Pour résoudre ce problème inverse on emploie principalement une approche "canonique" (pour résoudre le problème direct pendant l’inversion, on utilise un objet "équivalent" dont la solution est connue - à un ou plusieurs paramètres prés) l’approximation ICBA (Intersecting Canonical Body Approximation [7]) comme estimateur afin de reconstruire la fonction de contour d’un objet cylindrique acoustiquement pénétrable (ou impénétrale) à partir de données le plus généralement synthétiques (simulées par un autre algorithme). La reconstruction se fait très rapidement du fait que l’ICBA incorpore une solution connue d’avance du problème direct pour chaque jeu des paramètres d’essai, ce qui permet par exemple de suivre en temps réel les mouvements et les déformations de l’objet, comme, par exemple, en échographie ultrasonore d’un foetus.

Fig.3 : interface Matlab de pilotage du problème inverse 2D temps réel. Fig.3’ : reconstruction temps réel d’un corps en mouvement.

III. Choix d’une fonction coût.

D’une façon générale, une première approche consiste à résoudre (dans le plan réel ou complexe [7]) l’équation ou à chercher les minima de la forme quadratique associée avec,

Une fois les solutions trouvées, se pose le problème d’éliminer les solutions parasites pour n’en garder qu’une pour chaque direction de diffusion (image du haut de la Fig.4). Pour cela, nous avons d’abord développé des algorithmes de post-traitement prenant en compte l’information contenue dans la partie imaginaire des solutions (la recherche des minima se fait dans le plan complexe, [7]). Plus récemment, sur les bases de modélisations analytiques hautes fréquences, nous avons montré que le fait d’utiliser deux fréquences permet de discriminer une solution (image du bas de la Fig.4) [6].

Figs.4 : image du haut : dans le plan (xoy), ensemble des solutions générées pour deux fréquences de sondage et pour chaque direction de diffraction tout autour de la cible ; image du bas : résultat du post-traitement (trait continu : objet réel, points : objet reconstruit).

Une façon plus traditionnelle de procéder consiste à ajouter au terme un terme de pénalité [2] traduisant une mesure de l’erreur faite en satisfaisant les conditions aux limites [2] ou qui pénalise les écarts au point courant [7]. Cependant le poids à donner à ce deuxième terme par rapport au premier reste un ``art’’ à la mesure du ``savoir-faire’’ de l’expérimentateur (un mauvais choix conduit généralement à une mauvaise solution).

Nous nous sommes donc efforcés à rendre moins ``opérateur dépendant’’ le choix du terme de pénalité ainsi que le poids associé à celui-ci. Une méthode originale a été développée [5] permettant d’obtenir une fonction coût dont la valeur du minimum global correspond à la variable à reconstruire et cela, sans aucun paramètre numérique à ajuster. Le principe consiste à prendre en compte les contributions de plusieurs fréquences, la fonction coût devient la somme des fonctions coût obtenues pour chaque fréquence particulière (Fig.5.)

Deux fréquences suffisent en théorie, mais nous avons montré que quatre fréquences sont nécessaires [3] pour répondre à la plupart des cas.

Fig.5 : fonctions coût pour une direction de diffusion et pour chaque fréquence (lignes en traits pleins ou pontillés) à minima locaux et la fonction coût multifréquence (carrés) à minium global.

IV. Algorithmes génétiques.

Dès lors que nous sommes capables d’identifier nos inconnues comme celles réalisant le minimum global d’un fonction coût particulière, nous pouvons utiliser des algorithmes ``globaux’’ de recherche de minimum qui présentent l’avantage de ne pas converger vers des solutions locales parasites. Nous avons, sur ce thème, initié un travail de recherche [3] portant sur l’adaptation des algorithmes génétiques aux spécificités de notre problème (cf. Fig.6).

Fig. 6 : comparaison des reconstructions d’une cible elliptique en utilisant un algorithme génétique et un algorithme classique de minimisation (Levenberg-Marquardt).

V. Sensibilité aux paramètres numériques.

Les problèmes inverses non linéaires sont des problèmes mathématiquement mal posés. Nous essayons d’apporter des réponses à deux questions : 1) comment évaluer à priori l’influence d’une erreur sur une (ou plusieurs) donnée(s) sur la solution du problème ; 2) dans quelle mesure la fonction coût multifréquence que nous avons définie précédemment permet de stabiliser l’inversion ; 3) Quelle est la part de l’erreur de modèle dans les erreurs des paramètres reconstruits.

A titre d’exemple (Fig. 7), lorsque les données sont "exactes’’, la fonction coût est de l’ordre de 10E-17 et la solution trouvée est quasi exacte. Dès qu’on introduit une petite perturbation d’un des paramètres des données (erreur de quelques pourcents sur la célérité par exemple), la fonction coût devient de l’ordre de 10E-1 et l’erreur commise sur la solution trouvée est très grande (jusqu’à plusieurs dizaines de %).

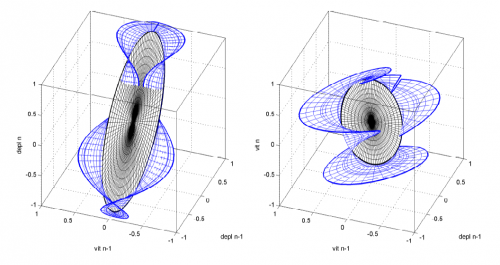Figs.7 : image du haut : fonction coût monofréquence avec des données ``saines’’, on trouve r=0.6 (exacte), b_3=9.328E-4 (exacte). Image du bas, données faiblement corrompues : on trouve r=0.546 (erreur =10%), b_3=8.355E-4.

VI. Simplification de l’estimateur.

Une partie importante de nos travaux porte sur la recherche d’approximations canoniques d’interaction onde objet, approximations que nous implémentons dans les processus d’inversion de façon à diminuer les temps de calculs sans pour autant perdre en précision. Sur le même principe que la méthode "icba" nous nous intéressons aujourd’hui à des milieux plus complexes (Fig.8) approchés par des modélisations multicouches.

Figs.8 : Approximations cannoniques sur des objets de forme quelconque (image du haut) ou des milieux ``granulaires’’ (image du bas).

Nous avons montré, avec la méthode du "corps canonique interceptant : icba") que l’on pouvait avantageusement tirer partie de telle simplification. Actuellement nos efforts portent sur des simplifications plus complexes, i.e., de milieux granulaire ou composites (cf Fig.8).

VII. Inadéquation de modèle.

Ces simplifications posent le problème de ce que nous appelons l’inadéquation de modèle, c’est à dire l’impossibilité de la configuration simplifiée de décrire tous les phénomènes qui se produisent dans le cas réel (Fig. 9). Une des démarches que nous avons mise au point pour compenser cette inadéquation, consiste à introduire une partie complexe à des variables bien réelles (par exemple le rayon d’un cylindre ou l’épaisseur d’une lame). La partie complexe peut être interprétée comme une mesure de l’erreur de modèle. Ceci nous permet d’avoir une ``approximation’’ de l’erreur de modèle commise.

Fig.9 : Exemple d’inadéquation de modèle, lame à faces parallèles.

VIII. Inversion multiparamètres.

Si nous commençons à maîtriser l’inversion sur un paramètre, la reconstruction simultanée de plusieurs inconnues (notamment le couplage d’inconnues géométriques et d’inconnues relatives à la nature physique de la cible) reste encore difficile. Pour améliorer nos images, nous développons la piste consistant à surdéterminer nos systèmes d’équations (par exemple pour la reconstruction de trois paramètres : densité, célérité et rayon d’un cylindre parfaitement circulaire nous utilisons N mesures différentes (N >> 3) du champs diffracté par exemple pour plusieurs fréquences).

Fig.10 : Reconstructions des contours interne et externe d’une cible non canonique.

IX. Problème inverse de milieux.

Le problème inverse de milieu pour un domaine cylindrique circulaire est étudié [4]. Nous avons démontré qu’au second ordre en ( le nombre d’onde dans le milieu hôte et le rayon du cylindre), seuls les trois premiers termes (i.e., les ordres 0, -1 et +1) dans le développement en ondes partielles du champ diffracté sont non nuls, et les paramètres matériels figurent dans ces termes de manière explicite. De plus, le terme d’ordre zéro ne contient que deux des paramètres inconnus (i.e., les parties réelle et imaginaire de la compressibilité complexe du cylindre ) tandis que les termes d’ordres ± 1 contiennent l’autre paramètre matériel (i.e., la densité du cylindre ). On développe une méthode, faisant appel à des données concernant la totalité de la fonction de diffusion en zone lointaine, qui donne lieu à des expressions explicites pour et . Cette méthode livre une estimation très précise de et même lorsque la fréquence de l’onde interrogatrice est telle que est aussi grand que (Figs. 11).

Figs. 11 : Diagrammes des erreurs relatives sur la reconstruction des variables (parties réelles et imaginaires) et

X. Bibliographie

[1] D. Colton, R. Kress. Inverse Acoustic and Electromagnetic Scattering Theory, Spring Verlag, 1992

[2] T.S. Angell, R.E. Kleinmann, B. Kok, GF Roach. A constructive method for identification of an impenetrable scatterer. Wave Motion, ( 11):185-200, 1989

[3] A. Mosbah. Développement d’algorithmes non lin’éaires pour l’imagerie acoustique. Mémoire de Master 2A, Université de la Méditerranée, 2006.

[4] T. Scotti, A. Wirgin. Reconstruction of the three mechanical material constants of a lossy fluid-like cylinder form low frequency scattered acoustic fields, C.R.Acad.Sci.Paris IIb, 332, 2004, 717-724.

[5] L. Le-Marrec, P. Lasaygues, T. Scotti, C. Tsogka. Efficient shape reconstruction of non-circular tubes using broadband acoustic measurements, Acta Acustica united with Acustica, 92:355-361, 2006.

[6] E. Ogam, T. Scotti, A. Wirgin. Non-uniqueness in connection with methods for the reconstruction of the shape of cylindrical bodies from acoustic scattering data. In A. Wirgin (ed.), Actes du colloque Acoustics mechanics and the related topics of mathematical analysis - AMRTMA. 2002. Fréjus (France) - 18-22 juin 2002 - World Scientific, A. Wirgin Ed.

[6’] E. Ogam, T. Scotti, A. Wirgin. Reduction of the ambiguity of shape reconstruction of cylindrical bodies using both real and synthetic acoustic scattering data. In Wirgin A. (ed), Actes du colloque Acoustics Mechanics and the Related Topics of Mathematical Analysis, pp 222—228. World Scientific, Singapore, 2002

[7] T. Scotti. Thèse de Doctorat. Localisation et reconstruction des caractéristiques géométriques et physiques d’un objet à l’aide du champ acoustique mesuré. 1997.

[8] T. Scotti, A. Wirgin. Reconstruction en temps-réel de la taille, position, orientation et forme d’un objet a partir de champs diffractes acoustiques. Journées gdr ondes, 8-10 décembre 2003, Marseille