This is a joint work with Mathias LEGRAND, McGill University and Sokly HENG, Royal Phnom Penh University.
The framework of nonlinear normal modes (NNM) is extremely powerful to investigate the nonlinear vibrations of mechanical systems. An autonomous thin vibrating rod in contact against a frictionless rigid foundation is investigated in the form of a N -dof harmonic oscillator subjected to a purely elastic impact rule which preserves the total energy. We show that this system features a continuous set of periodic orbits supported by non-smooth sub-manifolds in the phase portrait. The physical solutions are subjected to a one-sided condition. Moreover, the stability of this solution is considered.
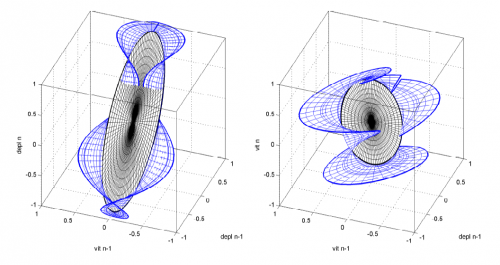
- Cross-section in the phase portrait of the invariant manifold supporting the second mode of vibration of a 3-dof spring-mass system undergoing one impact per period. Left : (u2, du2/dt, u3) ; right : (u2 , du2/dt , du3/dt). Black shows the linear behavior while blue shows the nonlinear behavior. Grazing occurs at the boundary separating the two behaviors.


