Slender structures can exhibit large shape-changes without large material deformations. In this regime, geometrical non-linearities play a crucial role and can be exploited to conceive reconfigurable structures for shape-control applications. In this talk, I will discuss the modelling of a class of shells with almost uniform curvature and I will show how to effectively control their shape by prescribing target inelastic curvatures associated to plastic deformations and embedded active materials.
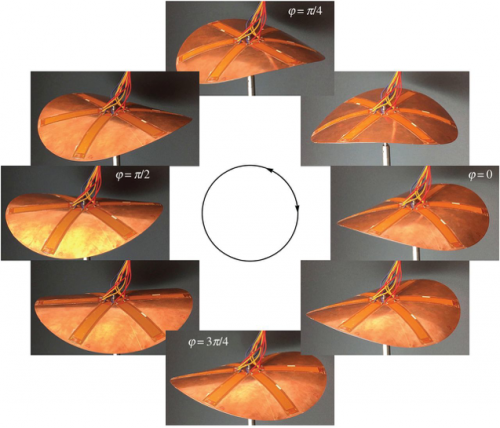 I will present a specific application consisting of a shell with a zero-stiffness deformation mode obtained by plastically deforming an initially flat copper disk, so as to induce large isotropic and almost uniform inelastic curvatures. The shell is theoretically neutrally stable, owning a continuous manifold of stable cylindrical shapes corresponding to the rotation of the axis of maximal curvature. Small imperfections render the actual structure bistable, giving preferred orientations. A three-parameter piezoelectric actuation allows us to add a small perturbation to the plastic inelastic curvature and to control the direction of maximal curvature. This actuation law is designed through a minimal fully non-linear inextensible uniform-curvature shell model.
I will present a specific application consisting of a shell with a zero-stiffness deformation mode obtained by plastically deforming an initially flat copper disk, so as to induce large isotropic and almost uniform inelastic curvatures. The shell is theoretically neutrally stable, owning a continuous manifold of stable cylindrical shapes corresponding to the rotation of the axis of maximal curvature. Small imperfections render the actual structure bistable, giving preferred orientations. A three-parameter piezoelectric actuation allows us to add a small perturbation to the plastic inelastic curvature and to control the direction of maximal curvature. This actuation law is designed through a minimal fully non-linear inextensible uniform-curvature shell model.
I will further discuss the extension of this work in two directions : (i) the understanding of the complex nonlinear dynamics of almost neutrally stable shells and (ii) and to fluid-structure interaction applications.
References
1. A video : https://doi.org/10.6084/m9.figshare...
2. Hamouche, W., Maurini, C., Vidoli, S., & Vincenti, A. (2017). Multi-parameter actuation of a neutrally stable shell : a flexible gear-less motor. Proceedings of the Royal Society of London A : Mathematical, Physical and Engineering Sciences, 473(2204). https://doi.org/10.1098/rspa.2017.0364
3. Seffen, K. A., & Maurini, C. (2013). Growth and shape control of disks by bending and extension. Journal of the Mechanics and Physics of Solids, 61(1), 190–204. https://doi.org/10.1016/j.jmps.2012...
4. Corsi, G., De Simone, A., Maurini, C., & Vidoli, S. (2019). A neutrally stable shell in a Stokes flow : a rotational Taylor’s sheet. Proceedings of the Royal Society A : Mathematical, Physical and Engineering Sciences, 475(2227), 20190178. https://doi.org/10.1098/rspa.2019.0178


