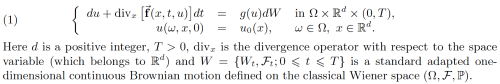Abstract
In this talk, I will present a joint work ([BCC20]) on the Cauchy problem for a nonlinear hyperbolic scalar conservation law in d space dimensions forced by a multiplicative stochastic noise (in the sense of Itô) and with a general time and space dependent flux-function of type :
The well-posedness theory for (1) is a known result since the work of [DeV10] by the way of a kinetic approach and the numerical approximation of its solution has been the subject of few work recently ([BCG16, M18]...). Our aim here is to address simultaneously theoretical and numerical issues. More precisely I will present an existence and uniqueness result of the
stochastic entropy solution of (1) together with its approximation by a finite volume scheme.
Comparing with the existing results on the subject, the true novelty of the present study is
the use of the numerical approximation to get both existence and uniqueness of the stochastic
entropy solution.
My talk will be separated in three parts. In a first one I will introduce the notion of stochastic
entropy solution for (1) as well as a generalized notion of solution (namely measure-valued
entropy solution). In a second one, I will present the monotone finite volume scheme used to
approximate (1). After deriving stability estimates satisfied by the finite volume approximation
(uT ; k), I will present its convergence towards a measure-valued entropy solution. The last part
will be devoted to show the uniqueness of this generalized solution as well as the existence
and uniqueness of the stochastic entropy solution for (1). The idea is to adapt the Kruzkhov
doubling variable technique to the stochastic case by comparing any generalized solution to
the finite volume approximation, having in mind the work of [BVW12].
References :
[BCC20] C. Bauzet, V. Castel, and J. Charrier. Existence and uniqueness result for an hyperbolic scalar conservation
law with a stochastic force using a finite volume approximation. To appear in Journal of Hyperbolic
Differential Equations.
[BCG16] C. Bauzet, J. Charrier, and T. Gallouët. Convergence of monotone finite volume schemes for hyperbolic
scalar conservation laws with a multiplicative noise. Stochastic Partial Differential Equations : Analysis and
Computations, Volume 4, 150-223, 2016.
[BVW12] C. Bauzet, G. Vallet, and P. Wittbold. The Cauchy problem for a conservation law with a multiplicative
stochastic perturbation Journal of Hyperbolic Differential Equations, Volume 9, Issue 4, 661-709,
2012.
[DeV10] A. Debussche and J. Vovelle. Scalar conservation laws with stochastic forcing. J. Funct. Anal.,
259(4):1014-1042, 2010.
[M18] A. Majee. Convergence of a
flux-splitting finite volume scheme for conservation laws driven by Lévy noise.
Applied Mathematics and Computation, 338(1) : 676-697, 2018.
Pendant cette période de retour progressif au travail en présentiel, le LMA organise une série de séminaires en visioconférence.
Les modalités de connexion :
Join the meeting :
https://meet.jit.si/SéminairevisioLMA
To join by phone instead, tap this : +1.512.647.1431,,1274960328#
Looking for a different dial-in number ? See meeting dial-in numbers : https://meet.jit.si/static/dialInIn...
If also dialing-in through a room phone, join without connecting to audio : https://meet.jit.si/Séminairevisio...